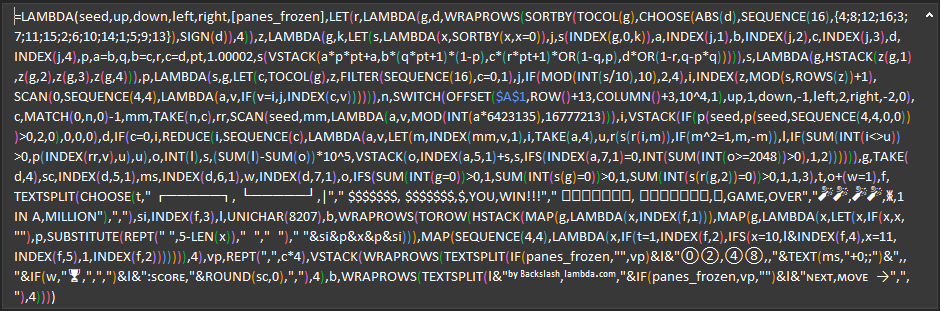
Excel Lambda port of the famous mobile game
Syntax: =\2048(seed, up, down, left, right, [panes_frozen]) => arrayExpand full code
=LAMBDA(seed,up,down,left,right,[panes_frozen],
LET(
// Get all the moves made so far by the player
moves_col, SWITCH(
INDIRECT("R[14]C[4]:R[10013]C[4]",0), // Get relative position of the inputs
up,1,
down,-1,
left,2,
right,-2, // note the value assigned to each move
0
),
moves_count, MATCH(0,moves_col,0)-1,
moves, TAKE(moves_col, moves_count),
// Create an array of pseudorandom numbers for rng after each move
randoms, SCAN(seed,moves,LAMBDA(a,v,MOD(a*6423135,16777213))),
// Locate empty spaces in the grid and put random 2's or 4's in them.
place_random, LAMBDA(seed, grid,
LET(
col, TOCOL(grid),
zeros, FILTER(SEQUENCE(16),col=0,1), // positions of 0's
digit, IF(MOD(INT(seed/10),10),2,4), // There is a 1/10 chance that the number placed will be a 4.
// int(seed/10) to remove correlation between tile placement and value
// otherwise a 4 would only ever appear on the 10th empty position
selected_index,
INDEX(
zeros,
MOD(seed, ROWS(zeros))+1
),
SCAN(0,SEQUENCE(4,4),LAMBDA(a,v,
IF(
v=selected_index,
digit,
INDEX(col,v)
)
))
)
),
// Initialize grid with two randomly placed 2's
// by repurposing our place_random function
start_grid, VSTACK(
IF(
place_random(seed,place_random(seed,SEQUENCE(4,4,0,0)))>0,
2,
0
),
0,0,0 // Stack 3 more rows at the end of the grid for total score, move score and victory status
),
// Rotation and sliding functions that do the heavy lifting
rotate, LAMBDA(grid,direction, // rotate by sorting by specific order
WRAPROWS(
SORTBY(
TOCOL(grid),
CHOOSE(ABS(direction),
SEQUENCE(16), // 0 or 180 degree rotation (no change or reverse)
{4;8;12;16;3;7;11;15;2;6;10;14;1;5;9;13} // 90 or 270 degrees (left or right)
),
SIGN(direction)
),
4
)
),
// Main game logic, what happens when you slide a single column
slide_column, LAMBDA(grid,column,
LET(
shift, LAMBDA(x,SORTBY(x,x=0)), // move all 0's to the end without disturbing the order of the numbers
j, shift(INDEX(grid,0,column)),
a,INDEX(j,1), b,INDEX(j,2), c,INDEX(j,3), d,INDEX(j,4),
p, a=b, q, b=c, r, c=d,
pt,1.00002, // modifier to store score resulting from merging numbers after the decimal point
shift(
VSTACK( // evil boolean arithmetic for brevity. Saves all of 38 characters, but looks impressive.
a*p*pt+a, // if(p,a*pt+a,a),
b*(q*pt+1)*(1-p), // if(p,0,if(q,a*pt+a,a)),
c*(r*pt+1)*OR(1-q,p), // if(and(not(p),q),0,if(r,c*pt+c,c)),
d*OR(1-r,q-p*q) // if(and(r,or(not(q),p)),0,d)
)
))
),
// apply slide_col to all columns in the grid.
slide, LAMBDA(grid,
HSTACK(
slide_column(grid,1),
slide_column(grid,2),
slide_column(grid,3),
slide_column(grid,4)
)
),
// Main game loop
game, IF(moves_count=0, start_grid,
REDUCE(start_grid,SEQUENCE(moves_count),LAMBDA(a,v,
LET(
move, INDEX(moves,v,1),
grid, TAKE(a,4),
unrotated,
rotate( // Step 3. unrotate grid
slide( // Step 2. slide grid
rotate(grid,move) // Step 1. rotate grid
),
IF(move^2=1,move,-move) // unrotation for moves 1 & -1 (0 and 180 rotation) is the same as rotation,
// unrotation for moves 2 & -2 (90 and 270 rotation) is the negative of rotation.
),
placed, IF(SUM(INT(grid<>unrotated))>0, // random tiles are only placed if the move resulted in a change to the grid
place_random(INDEX(randoms,v), unrotated),
unrotated
),
truncated, INT(placed), // sliding adds score after the decimal point, we remove it here
score, (SUM(placed)-SUM(truncated))*10^5, // calculate the sum of the score we removed.
VSTACK( // build up game data
truncated, // 4 rows of grid
INDEX(a,5,1) + score, // 1 cell with total score (index 5,1)
score, // 1 cell with current move score (index 6,1)
IFS(
INDEX(a,7,1)=0,INT(SUM(INT(o>=2048))>0), // 1 cell with victory status
1,2 // victory=1 occurs only on the turn when a victory occured, after that victory will equal 2
)
)
)
))
),
grid, TAKE(game,4),
score, INDEX(game,5,1),
move_score, INDEX(game,6,1),
win, INDEX(game,7,1),
game_over, IFS( // check for game over
SUM(INT(grid=0))>0,1, // if there are zeros, it's not game over
SUM(INT(slide(grid)=0))>0,1, // if there are zeros after sliding the grid, it's not game over
SUM(INT(slide(rotate(grid,2))=0))>0,1, // if there are zeros after rotating and sliding the grid, it's not game over
1,3 // otherwise it is game over (no game over is 1, game over is 3, look below why)
),
state, game_over+(win=1), // evil boolean arithmetic again for brevity
styling, TEXTSPLIT( // array of assets for grid styling and messages for special states
CHOOSE(state, // CHOOSE(o+(w=1),,,) saves 9 chars over IFS(AND(o,w=1),,o,,w=1,,1,)
" ┌─────┐, └─────┘,|", // 1, no game_over, no win
" $$$$$$$, $$$$$$$,$,YOU,WIN!!!", // 2, win, no game over
" ▒▒▒▒▒▒▒, ▒▒▒▒▒▒▒,▒,GAME,OVER", // 3, game over, no win
"🍾🍾,🍾🍾,ᛤ,1 IN A,MILLION" // 4, win and game over at the same time, technically possible but unlikely
),
","
),
edge,INDEX(styling,3),
rl, UNICHAR(8207), // right-to-left modifier. Invisible character, changes text direction, for right-aligning text in cell
styled, // add styling to grid
WRAPROWS( // ____________|1||2||3||4|^^^^^^^^^^^^ ____________
TOROW( // ____________|5||6||7||8|^^^^^^^^^^^^ becomes |1||2||3||4|
HSTACK( // ____________|9||0||1||2|^^^^^^^^^^^^ ^^^^^^^^^^^^ ...
MAP(grid,LAMBDA(x,INDEX(styling,1))), // ____
MAP(grid,LAMBDA(x, // |1||2|...
LET(
x, IF(x,x,""),
// add padding as narrow space, replace each 2 narrow spaces with 1 wide space
p, SUBSTITUTE(REPT(" ",5-LEN(x))," "," "),
" " & edge & p & x & p & edge // " |__2__|"
)
)),
MAP(SEQUENCE(4,4),LAMBDA(x,
IF(state=1,
INDEX(styling,2), // no special state, no message
IFS(
x=6,rl&INDEX(styling,4), // splice in message in the middle of the grid
x=7,INDEX(styling,5),
1,INDEX(styling,2)
)
)
)) //
)
),
4 // WRAPROWS
),
// assembling the whole game area
vpad, REPT(",",moves_count*4), // vertical padding to shift input row down or shift entire game down to input level, depending on [panes_frozen]
VSTACK(
WRAPROWS( // header
TEXTSPLIT(
IF(panes_frozen,"",vpad) &
rl & "⓪②,④⑧,," & TEXT(move_score,"+0;;") &
",," & IF(win,"🏆,",",") & rl & ":sᴄᴏʀᴇ," & ROUND(score,0),
","
),
4),
styled, // grid
WRAPROWS( // footer
TEXTSPLIT(
rl & "ᵇʸ ᴮᵃᶜᵏˢˡᵃˢʰ,ˡᵃᵐᵇᵈᵃꞏᶜᵒᵐ," &
IF(panes_frozen,vpad,"") &
rl & "ɴᴇxᴛ,ᴍᴏᴠᴇ →",","
),
4)
)))
About this port
This was a fun one. If you don’t know the original 2048, definitely take a look at it here. The game is extremely intuitive and addicting.
It is also a perfect fit for an Excel port, being turn-based and about numbers on a grid.
I set out with a few assumptions in mind. Firstly, I wanted the port to be an honest-to-god, pure Lambda adaptation, that would not have disappointed me once I found out how it worked. That means: no VBA or Office scripts, no Python, no EVALUATE shenanigans and no circular references. No clickbait trickery, just something anyone could copy-paste into any Excel 365 worksheet and have it just work.
I also wanted the game to be as playable as possible, so I the player shouldn’t be expected to take extra steps to save the game state between turns.
That only leaves one solution, which is what the port does: keep track of all the moves and rerun the entire game from the beginning on each subsequent move.
My second assertion was that I wanted the game to look reasonably appealing without any cell formatting. The game should be entirely contained within the Lambda function, and not in a particular worksheet.
Finally, I wanted the game to fit within the 2084-character limit of the Name Manager’s Refers To window, so a user can make it into a named formula without resorting to any macros. That last one was particularly difficult, but I managed to just about squeeze it in using some serious minification, without compromising any functionality.
With those constraints in mind, let’s see how the game works.
Deep Dive
On each move (or recalculation), the function does the following:
- Reads all of the player’s moves made so far (lines 3:13)
- Prepares a vector of deterministic, pseudorandom numbers for random number input (15:16)
- Initializes the grid with two starting 2’s randomly placed based on the seed provided (41:50)
- Applies each move to the grid, randomly placing a new 2 or 4 after each one (94:125)
- Checks the state of the board for victory or loss condition (119:121; 130:136)
- Formats the final state of the grid for output, applying special graphics if victory or loss occurs (137:174)
- Builds up the final game area and adds padding to shift the “next move ->” indicator down. (175:194)
Reading player’s moves:
moves_col, SWITCH(
INDIRECT("R[14]C[4]:R[10013]C[4]",0),
up,1,
down,-1,
left,2,
right,-2, // note the value assigned to each move
0
),
moves_count, MATCH(0,moves_col,0)-1,
moves, TAKE(moves_col, moves_count),
There isn’t anything special, although the SWITCH() function returning an array can be a little unintuitive, if you’re not used to array Excel.
Because the first argument of SWITCH is a vector, we’re getting back a vector.
moves_col becomes a translation of the user inputs. Up, down, left and right were passed to the Lambda as arguments, and we are translating the user inputs according to those arguments into 1,-1,2,-2 respectively. Indirect serves to get the user inputs in relation to the cell, in which the formula resides. What we’re getting back is a column of 10000 rows (an average game is some 1000 moves long, so 10x should suffice), 4 cells to the right and 14 cells down from the cell with the formula (where the “next move ->” points to).
In moves, we are trimming the range to include only first continuous range of valid moves.
Preparing random numbers
randoms, SCAN(seed,moves,LAMBDA(a,v,MOD(INT(a*6423135),16777213)))
We need a way to get reproducible randomness in the game. It cannot change on recalculation. The technique comes from my \RAND.STABLE() function. It’s a simple linear congruential generator, starting with a seed argument. We are making as many random numbers as there are moves made – that is how many we will need.
Initializing the grid
// Locate empty spaces in the grid and put random 2's or 4's in them.
place_random, LAMBDA(seed, grid,
LET(
col, TOCOL(grid),
zeros, FILTER(SEQUENCE(16),col=0,1), // positions of 0's
digit, IF(MOD(INT(seed/10),10),2,4), // There is a 1/10 chance that the number placed will be a 4.
// int(seed/10) to remove correlation between tile placement and value
// otherwise a 4 would only ever appear on the 10th empty position
selected_index,
INDEX(
zeros,
MOD(seed, ROWS(zeros))+1
),
SCAN(0,SEQUENCE(4,4),LAMBDA(a,v,
IF(
v=selected_index,
digit,
INDEX(col,v)
)
))
)
),
// Initialize grid with two randomly placed 2's
// by repurposing our place_random function
start_grid, VSTACK(
IF(
place_random(seed,place_random(seed,SEQUENCE(4,4,0,0)))>0,
2,
0
),
0,0,0 // Stack 3 more rows at the end of the grid for total score, move score and victory status
),
The place_random function is what is used later on to place random 2’s and 4’s after each move, but we can also use it to initialize the grid with two 2’s.
We initialize the grid by passing a 4×4 array of 0’s into the place_random function twice, and turning any 4’s that might appear back into a 2’s.
The place_random function first turns the grid into a column, then prepares a 1D array (vector) of positions of zeros, where 2’s or 4’s can be placed. The digit (2 or 4) is determined from the random seed (90% probability of a 2, 10% probability of a 4, following the actual 2048 game mechanics). The index of the new digit is randomly selected (according to the seed) from the indices of zeros. After that a new 4×4 grid is created by the SCAN function such that every cell is copied from the original grid, except the selected index, where the new digit is placed.
The start_grid gets 0 zeros appended to it, which are placeholders for information that will be kept there when the game progresses.
Applying moves to grid
This is where the magic happens. Let’s brake it down.
First the functions that perform the grid transformations triggered by sliding:
rotate, LAMBDA(grid,direction, // rotate by sorting by specific order
WRAPROWS(
SORTBY(
TOCOL(grid),
CHOOSE(ABS(direction),
SEQUENCE(16), // 0 or 180 degree rotation (no change or reverse)
{4;8;12;16;3;7;11;15;2;6;10;14;1;5;9;13} // 90 or 270 degrees (left or right)
),
SIGN(direction)
),
4
)
),
// Main game logic, what happens when you slide a single column
slide_column, LAMBDA(grid,column,
LET(
shift, LAMBDA(x,SORTBY(x,x=0)), // move all 0's to the end without disturbing the order of the numbers
j, shift(INDEX(grid,0,column)),
a,INDEX(j,1), b,INDEX(j,2), c,INDEX(j,3), d,INDEX(j,4),
p, a=b, q, b=c, r, c=d,
pt,1.00002, // modifier to store score resulting from merging numbers after the decimal point
shift(
VSTACK( // evil boolean arithmetic for brevity. Saves all of 40 characters, but looks impressive.
a*p*pt+a, // if(p,a*pt+a,a),
b*(q*pt+1)*(1-p), // if(p,0,if(q,a*pt+a,a)),
c*(r*pt+1)*OR(1-q,p), // if(and(not(p),q),0,if(r,c*pt+c,c)),
d*OR(1-r,q-p*q) // if(and(r,or(not(q),p),0,d)
)
))
),
// apply slide_col to all columns in the grid.
slide, LAMBDA(grid,
HSTACK(
slide_column(grid,1),
slide_column(grid,2),
slide_column(grid,3),
slide_column(grid,4)
)
),
The key concept here is that we don’t actually slide the grid in four separate directions. We only ever slide the grid “up”. We just rotate it beforehand, so that the direction we want to slide to becomes “up”, then slide and rotate it back.
Rotation is done by turning the grid into a column, then sorting according to a precalculated order. The calculation itself was omitted from the code – it turned out I could save characters by hard-coding the 90-degree rotated order, rather than calculating it. The formula to calculate it would be: MOD((x*4)-1,16)+1-INT((x-1)/4) applied to SEQUENCE(16). If direction is up (1), we are sorting the vectorized grid ascending by SEQUENCE(16), so essentially doing nothing. If direction is down (-1), we are sorting descending by SEQUENCE(16) – so, reversing. If direction is left (2), we are sorting ascending by the hard-coded, 90 degree rotated order, if it’s right (-2), we are sorting by the reverse of that.
The slide_column function is what does the actual sliding, and is applied to one column at a time. The slide function applies the slide_column function to each column separately and stacks the results. You might think this is code duplication, but it actually saves a lot of characters comparing to TAKE(REDUCE(0,SEQUENCE(4),LAMBDA(a,v,HSTACK(a,slide_column(grid,v)))),-4), given that the slide_column(grid,n), part gets minified to s(g,n), in the final Lambda. Sometimes code duplication is the right thing to do.
Slide_column first shifts all the 0’s to the bottom by sorting. Then assigns single-letter variable names to the values in the column and to the results of their comparisons, so that they’re easier to work with. Then it does the actual sliding in a single pass by means of just pure, overly complicated logic. The arrays in Excel formula language (and all variables for that matter) are essentially immutable, i.e. you can’t change their value once you declare them, you can’t just loop through and modify the vector as you would in another programming language. You can loop over one array building up another one, but you cannot look back over what you’ve built or ahead on each iteration. I suppose it could be possible with some nested SCAN functions and multiple iterations to avoid the logical mess that is this function, but that would only change logical incomprehensibility to a functional one, and would most likely be slower.
Let’s break the logic down:
Here is our column:[1] -> If [1]=[2], [1] gets doubled, points get added, else no change.
[2] -> If [1]=[2], [2] becomes 0, otherwise if [2]=[3], [2] gets doubled, points get added, else no change.
[3] -> If [1]<>[2] (2 didn't become zero) and [2]=[3], [3] becomes 0, otherwise if [3]=[4], [3] gets doubled, points get added, else no change.
[4] -> If [1]=[2] or [2]<>[3] ([3] didn't become 0) and [3]=[4], [4] becomes 0, else no change.
The last step is to shift everything up by moving the zeros to the end again.
If two numbers are combined, points get added to the score. The number of points is equal to the value of the combined numbers. To keep track of the points, they are recorded after the decimal point in the resulting grid by means of the *pt modifier in the logic. They will be stripped, multiplied back to whole numbers and recorded later on.
Main game loop
game, IF(moves_count=0, start_grid,
REDUCE(start_grid,SEQUENCE(moves_count),LAMBDA(a,v,
LET(
move, INDEX(moves,v,1), // I don't understand why the ,1 has to be here, but it does.
grid, TAKE(a,4),
unrotated,
rotate( // Step 3. unrotate grid
slide( // Step 2. slide grid
rotate(grid,move) // Step 1. rotate grid
),
IF(move^2=1,move,-move) // unrotation for moves 1 & -1 (0 and 180 rotation) is the same as rotation,
// unrotation for moves 2 & -2 (90 and 270 rotation) is the negative of rotation.
),
placed, IF(SUM(INT(grid<>unrotated))>0, // random tiles are only placed if the move resulted in a change to the grid
place_random(INDEX(randoms,v), unrotated),
unrotated
),
truncated, INT(placed), // sliding adds score after the decimal point, we remove it here
score, (SUM(placed)-SUM(truncated))*10^5, // calculate the sum of the score we removed.
VSTACK( // build up game data
truncated, // 4 rows of grid
INDEX(a,5,1) + score, // 1 cell with total score (index 5,1)
score, // 1 cell with current move score (index 6,1)
IFS(
INDEX(a,7,1)=0,INT(SUM(INT(o>=2048))>0), // 1 cell with victory status
1,2 // victory=1 occurs only on the turn when a victory occured, after that victory will equal 2
)
)
)
))
),
grid, TAKE(game,4),
score, INDEX(game,5,1),
move_score, INDEX(game,6,1),
win, INDEX(game,7,1),
Main game loop is where all the moves made so far by the player get applied to the initial grid, where the extra random tiles are inserted, the score is tallied and the victory condition is checked.
We start by returning the start_grid if there haven’t been any moves made yet. That is because Excel doesn’t allow us to reduce over an empty sequence. In fact, it’s because we can’t have an empty sequence at all. SEQUENCE(0) just returns a #CALC! error.
In the loop, we get our current move and our grid. We rotate our grid according to the move, then slide and rotate it back.
We compare our processed grid to its previous state to see if any change was affected. If so, we place the random tiles in.
We remove the score recorded after the decimal point and record it in the score variable.
We stack our grid with total score, score from the last move, and the result of a check for a victory, and pass that bundle to the next loop iteration.
We only check for victory if no victory occurred on previous moves (victory state is 0). If victory occurred on the current move, the victory state becomes 1. If victory occurred on a previous move (victory state is not 0), we set the victory state at 2. This is so that the victory message only appears on the move that the victory occurred on, but previous victory is still visible during the game in the form of a little trophy emoji under the logo if the player decides to keep going after getting 2048.
After completing our main game loop, we liberate the components of the accumulator bundle into the final values for grid, score, move_score and win variables.
We are done with our essential game logic, all that comes after is just styling.
Check loss condition
Loss condition check is also just styling. Game Over occurs when no move can result in a change to the grid, so if we were to just leave a player without any indication that they lost, they would figure it out after at most 2 more moves.
game_over, IFS( // check for game over
SUM(INT(grid=0))>0,1, // if there are zeros, it's not game over
SUM(INT(slide(grid)=0))>0,1, // if there are zeros after sliding the grid, it's not game over
SUM(INT(slide(rotate(grid,2))=0))>0,1, // if there are zeros after rotating and sliding the grid, it's not game over
1,3 // otherwise it is game over (no game over is 1, game over is 3, look below why)
),
state, game_over+(win=1), // evil boolean arithmetic again for brevity
styling, TEXTSPLIT( // array of assets for grid styling and messages for special states
CHOOSE(state, // CHOOSE(o+(w=1),,,) saves 9 chars over IFS(AND(o,w=1),,o,,w=1,,1,)
" ┌─────┐, └─────┘,|", // 1, no game_over, no win
" $$$$$$$, $$$$$$$,$,YOU,WIN!!!", // 2, win, no game over
" ▒▒▒▒▒▒▒, ▒▒▒▒▒▒▒,▒,GAME,OVER", // 3, game over, no win
"🍾🍾,🍾🍾,ᛤ,1 IN A,MILLION" // 4, win and game over at the same time, technically possible but unlikely
),
","
),
We check loss condition by doing exactly that. Two moves, one up and one left. If no change to the grid occurs, it’s game over.
The IFS() function stops evaluation on the first true statement, so in most cases we won’t actually be doing any extra slides, as the first check is if there are any 0’s left on the grid.
The game_over variable value is set at 1 for no game over and at 3 for game over so that it can be efficiently combined with the integer value of win=1 (1 is true, 0 is false) for a nice integer in the range 1 to 4 to hang a CHOOSE function from. This is all in the name of saving characters.
The CHOOSE function selects the styling for the grid. During regular gameplay, we get some box art around the numbers, and victory and loss result in some other graphical effects and messages.
It is also technically possible to win and lose on the same turn, which, come to think of it, may not be as unlikely as I originally expected. In any case, the chance is definitely greater than 1 in a million.
Styling holds an array of style elements to be spliced into the grid in the following step.
Style output
edge,INDEX(styling,3),
rl, UNICHAR(8207), // right-to-left modifier. Invisible character, changes text direction, for right-aligning text in cell
styled, // add styling to grid
WRAPROWS( // ____________|1||2||3||4|^^^^^^^^^^^^ ____________
TOROW( // ____________|5||6||7||8|^^^^^^^^^^^^ becomes |1||2||3||4|
HSTACK( // ____________|9||0||1||2|^^^^^^^^^^^^ ^^^^^^^^^^^^ ...
MAP(grid,LAMBDA(x,INDEX(styling,1))), // ____
MAP(grid,LAMBDA(x, // |1||2|...
LET(
x, IF(x,x,""),
// add padding as narrow space, replace each 2 narrow spaces with 1 wide space
p, SUBSTITUTE(REPT(" ",5-LEN(x))," "," "),
" " & edge & p & x & p & edge // " |__2__|"
)
)),
MAP(SEQUENCE(4,4),LAMBDA(x,
IF(state=1,
INDEX(styling,2), // no special state, no message
IFS(
x=6,rl&INDEX(styling,4), // splice in message in the middle of the grid
x=7,INDEX(styling,5),
1,INDEX(styling,2)
)
)
)) //
)
),
4 // WRAPROWS
),
Applying style to the grid, we first stack horizontally a 4×4 array of just the repeated top edges of our numbers, the 4×4 grid of our numbers with added side edges and padding, and the 4×4 array out just the bottom edges. Bottom edges of numbers with the indices 6 and 7 (in the middle of the 2nd row of the grid) are replaced with the special message in case a win or game-over occurs.
We then turn our resulting array into one row of numbers, and then wrap rows again, resulting in the 3 initial arrays being shuffled together.
When making the padding for the numbers, two unicode characters are used – a narrow (1/4 em) space and a wide (1/2 em) space. All padding is done using the narrow spaces, each 2 narrow spaces are then substituted with a wide space. The character widths for different font sizes are all a mess, and a wide space is more likely to be equal in width to a single box-drawing character than 2 narrow spaces for each font size.
There is only one unicode character used throughout the entire lambda that is not just embedded into the code as a string literal, and that is the variable rl – the right-to-left modifier. It’s an evil character that makes text go backwards. It is used throughout the lambda to right-align text in cells without actually changing their formatting, but I wasn’t brave enough to paste the literal into the formula bar to see what would happen, even though it would save some 20 characters in the final version.
Build up and print game area
// assembling the whole game area
vpad, REPT(",",moves_count*4), // vertical padding to shift input row down or shift entire game down to input level, depending on [panes_frozen]
VSTACK(
WRAPROWS( // header
TEXTSPLIT(
IF(panes_frozen,"",vpad) &
rl & "⓪②,④⑧,," & TEXT(move_score,"+0;;") &
",," & IF(win,"🏆,",",") & rl & ":sᴄᴏʀᴇ," & ROUND(score,0),
","
),
4),
styled, // grid
WRAPROWS( // footer
TEXTSPLIT(
rl & "ᵇʸ ᴮᵃᶜᵏˢˡᵃˢʰ,ˡᵃᵐᵇᵈᵃꞏᶜᵒᵐ," &
IF(panes_frozen,vpad,"") &
rl & "ɴᴇxᴛ,ᴍᴏᴠᴇ →",","
),
4)
)))
The game area consists of padding (vpad, above or below the grid, depending on the [panes_frozen] optional argument value), the 2048 logo made up of circled digits, the move_score print out appearing on each move if points were earned, the optional emoji trophy if 2048 was achieved, the total score indicator, the grid, the footer (credit) and the next move indicator.
The TEXTSPLIT() with WRAPROWS() combo is used instead of just TEXTSPLIT() with different row and column delimiters, as it makes it easier to assemble vpad. If vpad occurs in the footer (if panes_frozen is true) the vpad gets broken unevenly, starting at column 3, ending on column 2, and would therefore have to be constructed differently than for the header, where it starts on column 1 and ends on column 4.
Using TEXTSPLIT() for this was not my initial idea, it still makes me a little uncomfortable to assemble strings just to split them into arrays again, especially strings of arbitrary length like vpad. However, VSTACK() is even worse, given that you can’t stack empty arrays (or have empty arrays at all), building logic to stack things that may or may not exist becomes even more clunky.
I also resent the idea of having emoji literals in the code, but it saves a ton of characters compared to declaring everything with UNICHAR().
Final Chapter: Minification
The logic presented here was written to be as concise as possible, often resulting in compromises to readability, but that is part of the fun with exercises in constrained programming such as this. This code, when stripped of all whitespace and comments, still stands at 2558 characters, well above the 2084 limit for the Refers To window. However, converting all variable names (except arguments, which are exposed to the user) to single or double letters netted me 1904 characters, somewhat below the design limit (within 10%). I’m happy to say that this was achieved with no compromises to functionality whatsoever and there simply isn’t anything left to add.
That, however, is nothing more than a happy coincidence, as I don’t really see any chance of going down more than maybe another 10% on character count. This only proves that this port was a perfect choice of project for my Excel hobby and skill level. I’d be happy to see someone attempt a better take on the slide algorithm in Excel. When you do, just remember: 2,2,2,2 goes to 0,0,4,4 and not 0,0,0,8.